Бір күні, алыста, далада, батыл Алдар Көсе ұлы саяхатқа шықты. Ол Бермуд үшбұрышын айналып өткеннен кейін, танымал Қазақ үшбұрышын зерттеуге шешім қабылдады. Бұл үшбұрыш Қазақ даласында орналасқан, Алдар Көсе үшбұрышқа кіруді жоспарлап отыр.

Қазақ үшбұрышы \(n-1\) аймаққа (климат, жер бедері түрі және т. б.) бөлінген, \(2, \ldots, n\) нөмірленген, ал дала аймақ №1 болып саналады. Аймақтар сызықтармен шектелген, сондықтан әр аймақ үшбұрыш (мүмкін қисық қабырғалармен) болып табылады, ал аймақтар қиылыспайды, әр сызық дәл екі түрлі үшбұрыштың қабырғасы болып табылады. Басқаша айтқанда, бүкіл дала – шексіз жазықтық, ал аймақтар планарлы триангуляцияны құрайды: жазықтықта сызықтар қиылыспайтын және әр беті үшбұрыш болатын планарлы граф (сыртқы бетін қоса алғанда). Мұндай конфигурацияны дала картасы деп атаймыз.

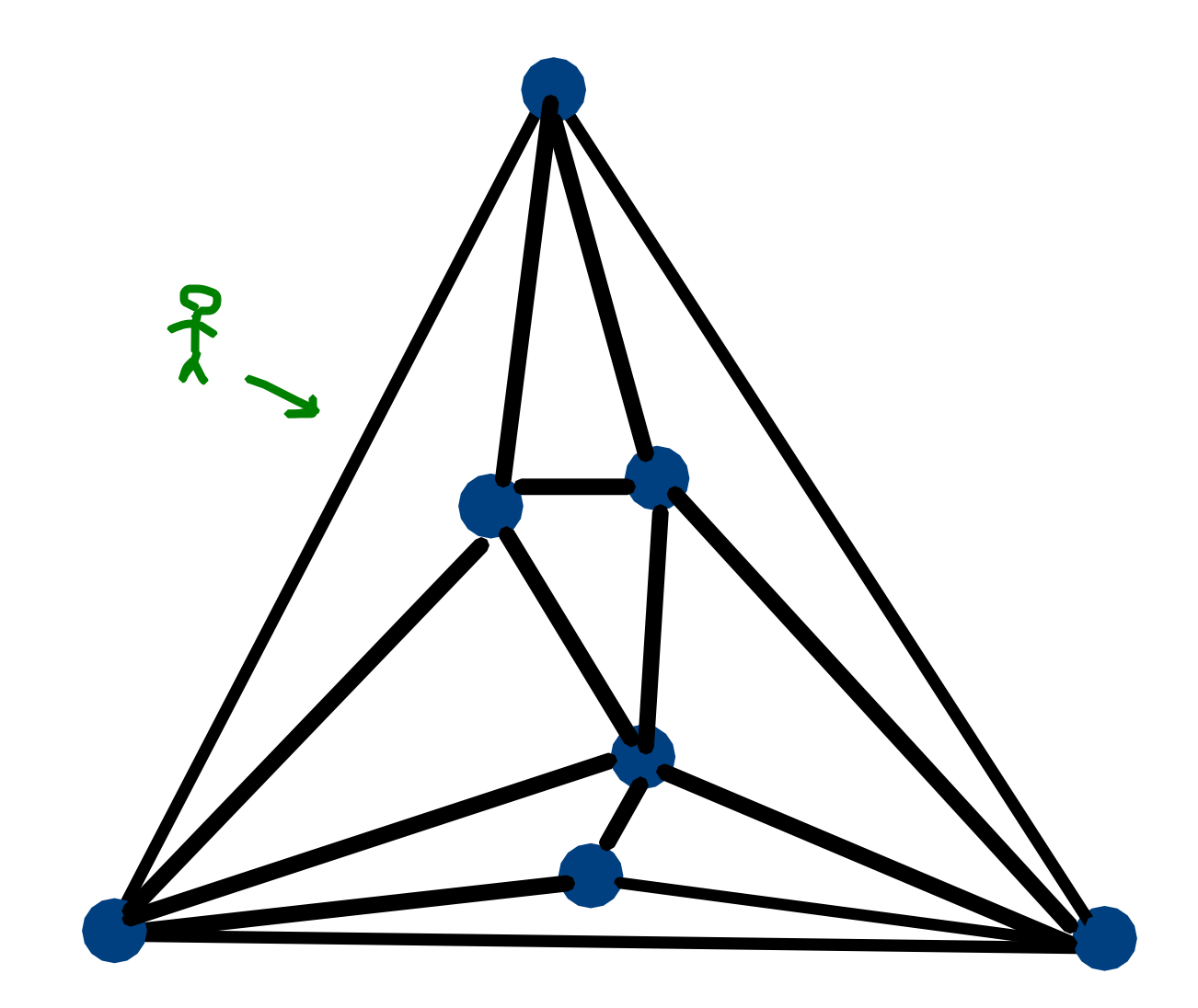Дала картасының мысалы, жасылмен Алдар Көсе даласында белгіленген.

Алдар Көсенің қарапайым жоспары бар: ол далада (аймақ 1) жолын бастайды, \(i=1,\ldots,n-1\) үшін аймақ \(i\)-ден аймақ \(i+1\)-ге қарай қозғалады, және соңында аймақ \(n\)-нен аймақ \(1\)-ге қайта оралады. Яғни, ол берілген тәртіпте әр аймақты дәл бір рет аралайды және қайтадан далаға шығады. Аймақтар арасында өтпелі байланыс тек солардың арасында ортақ қабырға болғанда мүмкін (ортақ қабырғалар 2 болуы мүмкін, әрқайсысы өз маршрутын тудырады). Алдар Көсенің маршруты – үздіксіз жабық қисық.

Өкінішке орай, біздің кейіпкерімізде дала картасы жоқ. Оған жолмен бірге салынған эквивалентті емес дала карталарының санын анықтауға көмектесіңіз, яғни \((M,P)\) жұптарының санын – карта \(M\) және аймақ \(i\)-ден аймақ \(i+1\)-ге өтетін және далаға қайта оралатын жол \(P\). Екі жұп \((M_1,P_1)\) және \((M_2, P_2)\) эквивалентті болып табылады, егер бір жұпты (карта, маршрут) екінші жұпқа айналдыратын сызықтардың үздіксіз түрленуі (аймақтардың сызықтарының деформациясы және шығыссыз қозғалыс, маршруттың деформациясы маршруттың өтулерін өзгертпейтін, жазықтықтың айналуы мен шағылуы) бар болса.

Енгізу

Бір жолда бір сан \(n\) (\(2 \le n \le 10^5\)) – аймақтар саны.

Шығару

Бір ғана сан – салынған маршрутпен эквивалентті емес карталардың саны. Мұндай сан тым үлкен болуы мүмкін, сондықтан оны \(10^9 + 7\) модулінде шығарыңыз.

Мысалдар

Енгізу 1

2

Жауап 1

1

Енгізу 2

3

Жауап 2

0

Енгізу 3

4

Жауап 3

5

Ескертпелер

Барлық карталар маршруттармен мысалдар. Қызылмен маршруттар, жасылмен – аймақтардың нөмірленуі.

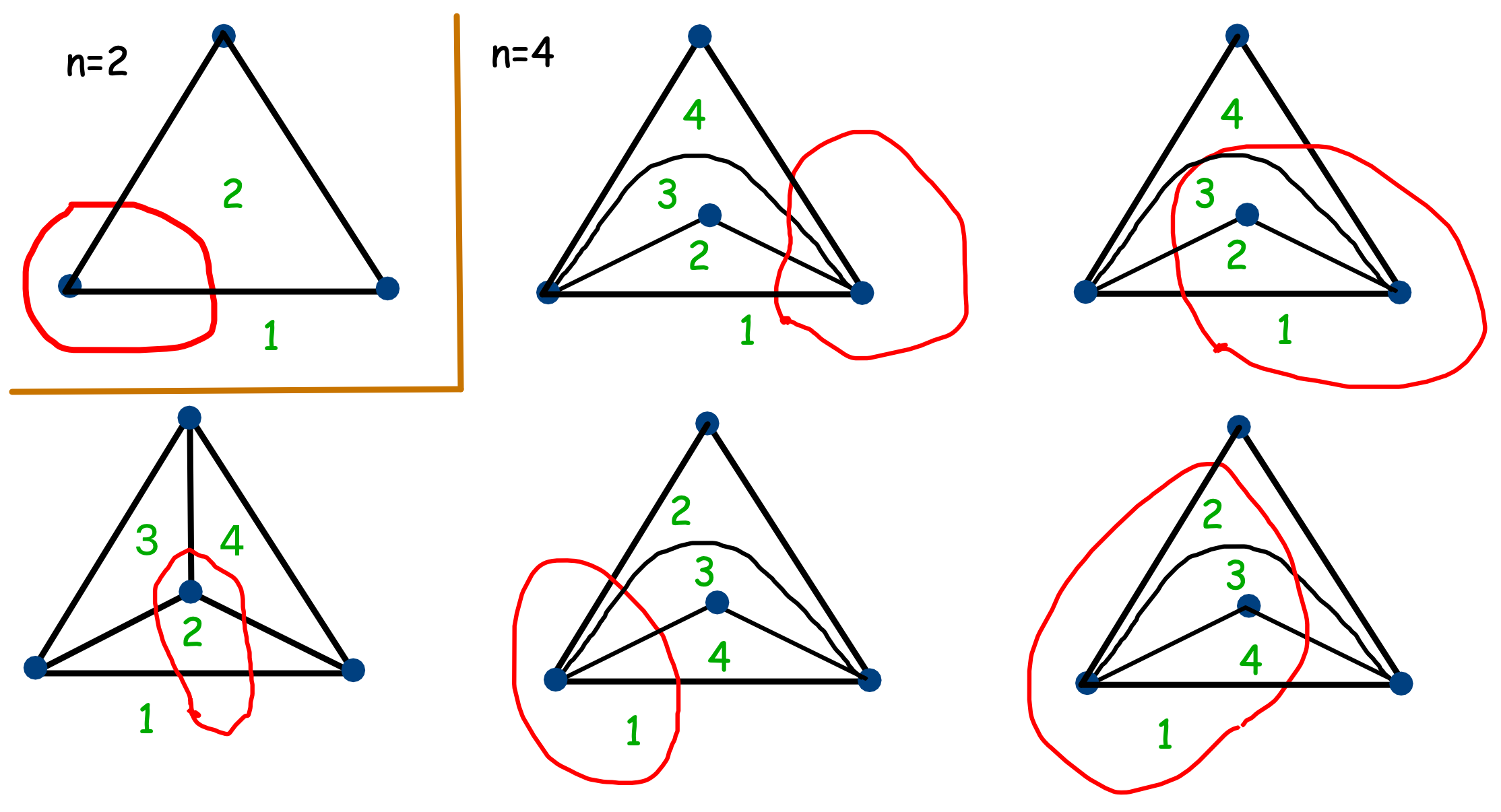
\(n=2\) үшін тек бір карта және эквиваленттілікке дейін бір ғана маршрут бар.

\(n = 4\) үшін 2 түрдегі карталар бар: бірінде 4 маршрут табылды, екіншісінде 1. Бұл \(5\) картаның маршрутпен эквивалентті емес екенін көрсетуге болады, және басқа жоқ.