Сізге мөлшері \(n \times m\) болатын \(A\) матрицасы берілген. \(1\)-ден \(n \times m\)-ге дейінгі әр бүтін сан матрицада нақты бір рет кездеседі.

Сізден осы матрицада келесідегідей қанша тіктөртбұрыш бар екенін санау керек:

• Тіктөртбұрыштың нақты \(4\) бұрышы бар. Басқаша айтқанда, тіктөртбұрыштың ені мен ұзындығы кем дегенде \(2\) болу керек.

• Егер бұрыштарды өсу ретімен орналастырып, көршілерін байланыстырса, онда ілмек пайда болады. Бұрыштарды өсу ретімен \(A\), \(B\), \(C\), \(D\) деп белгілейік. Ілмек пайда болу үшін \(A\) мен \(B\) қарама-қарсы бұрыштар болу керек және \(C\) мен \(D\) қарама-қарсы бұрыштар болу керек (мысалдарға түсіндірмені қараңыз).

Input

Бірінші жолда екі бүтін сан \(n\) және \(m\) берілген (\(1 \le n \times m \le 10^6\)).

Келесі \(n\) жолдың әрқайсысында дәл \(m\) бүтін сан берілген — \(A\) матрицасының мәндері (\(1 \le A_{i,j} \le n \times m\)).

\(1\)-ден \(n \times m\)-ге дейінгі әр бүтін сан матрицада нақты бір рет кездесетіндігіне кепілдік беріледі.

Output

Бір бүтін сан шығарыңыз — бұрыштарынан ілмек пайда болатын тіктөртбұрыштардың саны.

Sample Input 1

2 2
1 3
4 2

Sample Output 1

1

Sample Input 2

2 2
1 2
3 4

Sample Output 2

0

Sample Input 3

5 5
12 10 18 25 6
15 5 13 14 11
17 4 7 16 8
3 21 9 22 20
1 23 19 24 2

Sample Output 3

31

Notes

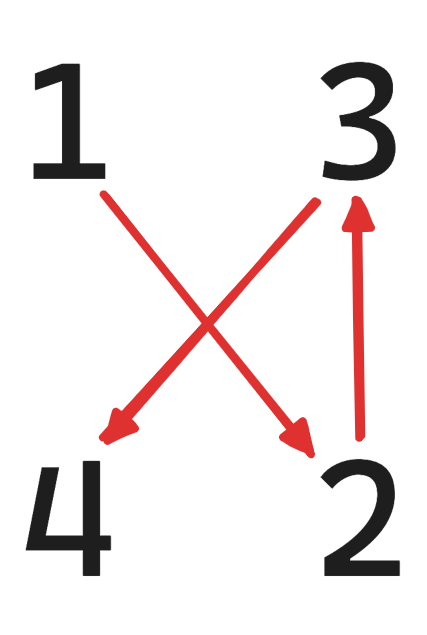
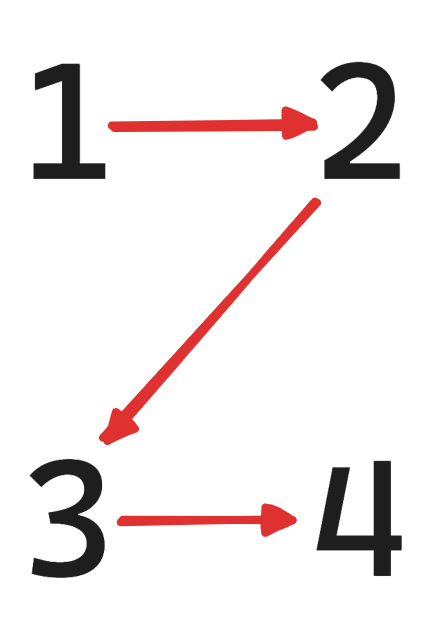
Бірінші мысалда ілмек пайда болады, ал екіншіде пайда болмайды