Қызыл-қара дарақ
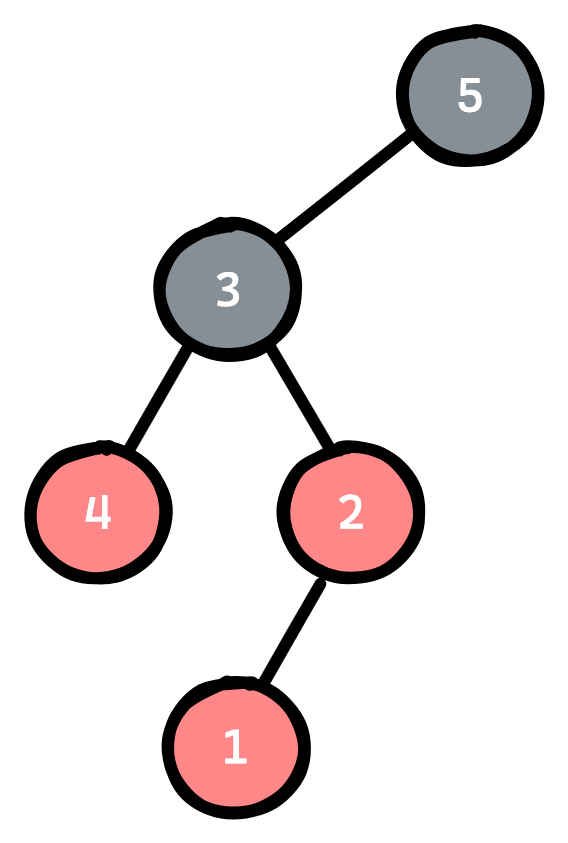
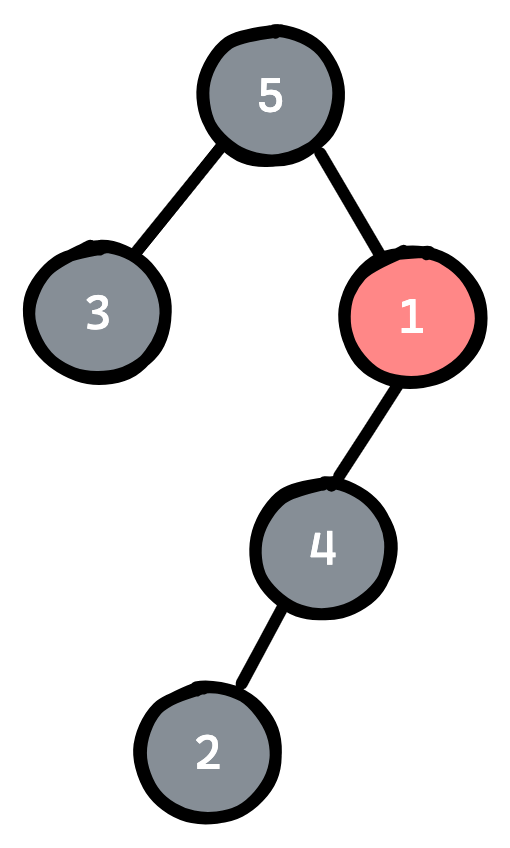
Сізге \(n\) төбеден тұратын дарақ және бір бүтін \(k\) саны беріледі. Дарақтың дәл \(k\) төбесі қызыл түсті, қалғандары қара түсті.
Сіздің міндетіңіз — әрбір қызыл төбелер жұбының арасындағы қашықтықтардың қосындысы максималды болуы үшін дарақтағы барлық қызыл төбелерді жұптарға бөлу. \(a\) және \(b\) төбелерінің арасындағы қашықтық \(a\) және \(b\) төбелерінің арасындағы жалғыз қарапайым жолдағы қырлардың саны ретінде анықталады.
Есептің жауабы ретінде әрбір қызыл төбелер жұбының арасындағы қашықтықтардың максималды қосындысын белгілейік. Бастапқыда \(k\) – тақ сан, сондықтан жауап анықталмаған. Барлық \(v\) төбелері үшін (\(1 \le v \le n\)), егер \(v\) төбесінің түсін қызылдан қараға немесе керісінше ойша өзгертетін болсақ, есептің жауабы неше болатынын есептеу керек (төбенің түсін өзгерткеннен кейін қызыл төбелердің саны жұп болады және жауап әрқашан анықталады).
Input
Әр тестте бірнеше кіріс жиынтығы бар.
Бірінші жолда бір бүтін \(t\) (\(1 \le t \le 100\)) — кіріс жиынтықтарының саны бар. Келесі жолдарда әрбір кіріс жиынтығының сипаттамасы берілген.
Жиынтықтың бірінші жолда екі бүтін \(n\) және \(k\) сандары бар — дарақтардың төбелерінің саны және қызыл түске боялған төбелердің саны (\(2 \le n \le 3 \cdot 10^5\), \(1 \le k \le n\), \(k\) – тақ сан).
Келесі \(n-1\) жолда \(u_i\) және \(v_i\) бар — дарақтың қырлары (\(1 \le u_i, v_i \le n\), \(u_i \neq v_i\)).
Келесі жолда \(n\) бүтін сан \(c_1, \ldots, c_n\) — барлық төбелердің түстері бар (\(0\) – қара, \(1\) – қызыл).
Енгізілген деректердің барлық жиынындағы \(n\) сомасы \(3 \cdot 10^5\) аспайтынына кепілдік беріледі.
Output
Әрбір кіріс жиынтығы үшін, \(n\) сан \(a_1, \ldots, a_n\) шығарыныз. \(a_i\) — \(i\) төбесінің түсін қызылдан қараға немесе керісінше ойша өзгертетін болсақ есептің жауабы.
Sample Input 1
2
5 3
4 3
2 3
1 2
3 5
1 1 0 1 0
5 1
3 5
5 1
1 4
4 2
1 0 0 0 0Sample Output 1
2 3 4 1 5
0 2 2 1 1Notes
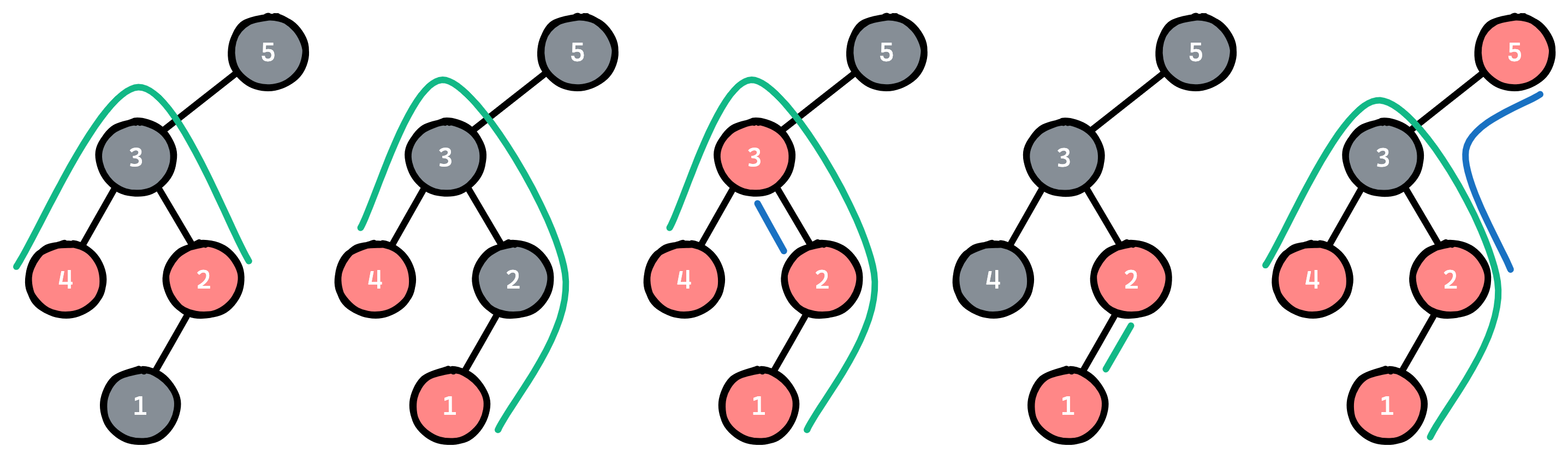
Пікірлер