Жақында Арманға құрылыс ойынын сыйлаған. Оны бүгін ол бірінші рет ойнайын деп жатыр.

Жинақта \(n\) жолдары мен \(m\) бағандарынан тұратын \(A\) кестесі бар. Кестенің әрбір ұяшығы бастапқыда бос. Арманда \(1\)-ден \(n \times m\)-ге дейінгі сандары бар дорба бар. Әр сан дорбада дәл бір рет кездеседі.

Ойын шарты бойынша Арман кестенің әр ұяшығында дәл бір сан болатындай етіп кестені осы сандармен толтыруы керек. Арман әр жол мен бағандағы жай сандардың қосындысы жұп болатындай сандарды орналастырса, ол ойында жеңіске жетеді.

Арманға ойынды жеңуге көмектесіңіз немесе оған бұл мүмкін емес екенін айтыңыз.

Input

Әр тестте бірнеше кіріс жиынтығы бар.

Бірінші жолда бір бүтін \(t\) (\(1 \le t \le 100\)) — кіріс жиынтықтарының саны бар. Әрбір кіріс жиынтығы бір жолдан тұрады.

Кіріс жиынтығының бірінші және жалғыз жолында екі бүтін \(n\) және \(m\)(\(1 \le n, m \le 100\)) — кесте өлшемдері бар.

Енгізілген деректердің барлық жиынындағы \(n \times m\) сомасы \(10\, 000\) аспайтынына кепілдік беріледі.

Output

Әрбір кіріс жиынтығы үшін Арман ойынды жеңе алса, 'YES' шығарыңыз, әйтпесе 'NO' шығарыңыз.

Арман ойында жеңіске жете алса, келесі \(n\) жолда кестенің өзін шығарыңыз. Әрбір жолда дәл \(m\) бүтін сан болуы керек. \(1\) мен \(n \times m\) аралығындағы әрбір сан кестеде дәл бір рет кездесуі керек. Әрбір жолдағы және әр бағандағы барлық жай сандардың қосындысы жұп болуы керек.

Sample Input 1

2
5 5
2 1

Sample Output 1

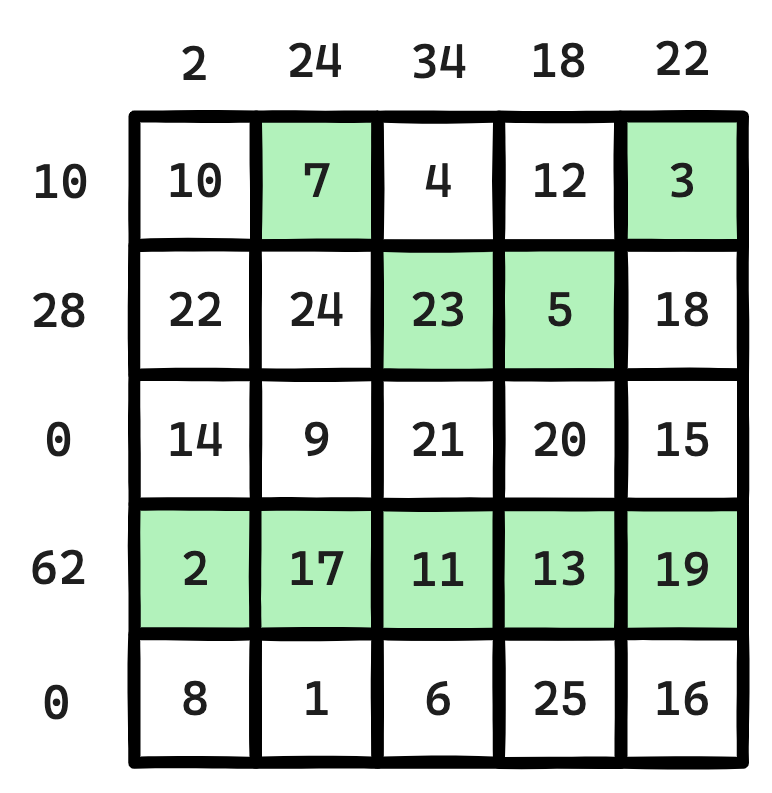
YES
10 7 4 12 3
22 24 23 5 18
14 9 21 20 15
2 17 11 13 19
8 1 6 25 16
YES
2
1

Notes

\(x\) жай сан деп аталады, егер оның дәл екі бөлгіші болса — \(1\) және \(x\) санының өзі.