Жарасханның донаты (ағылшын donut) бар, оны кесіп, ЧРК қатысушыларына таратуы керек.

Донат екі дөңгелек көпбұрыш арасындағы аймақпен анықталады:

• \(a\) төбесі бар сыртқы көпбұрыш \(A_1, A_2, \dots, A_a\);

• \(b\) төбесі бар ішкі көпбұрыш \(B_1, B_2, \dots, B_b\),

мұнда ішкі көпбұрыш сыртқы көпбұрыштың ішінде орналасқан.

Әр көпбұрыштың төбелерінің нумерациясы айналмалы тәртіппен (сағат тілімен немесе сағат тіліне қарсы) жүргізіледі.

Донатты кесудің көптеген тәсілдері бар. Алайда Жарасхан донатты кесудің дұрыс тәсілін түсінді: оны кесу үшін кесулерді қолдану керек, олар келесі шарттарға сәйкес келуі тиіс:

1. Әр кесу дәл бір сыртқы көпбұрыштың төбесі \(A_i\) мен дәл бір ішкі көпбұрыштың төбесі \(B_j\) арасын байланыстырады.

2. Кесулер кез келген болуы мүмкін (міндетті түрде тік емес), бірақ олар қиылыспауы және басқа төбелер немесе көпбұрыштың жақтары арқылы өтпеуі тиіс.

3. Әр алынған бөлік дәл үш сызықпен шектеледі, мұнда сызық – бұл көпбұрыштың бір жақтарының немесе кесу сызығының бірі.

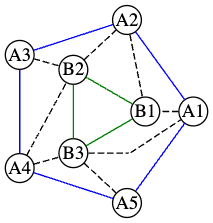
Донатты дұрыс кесіп, аспаздық технологиялар арқылы оларды мінсіз үшбұрыштарға айналдырады.

Жарасхан кесудің ең жақсы тәсілін түсінгісі келеді, сондықтан ол сұрайды: донатты дұрыс кесудің қанша тәсілі бар?

Екі «дұрыс» кесу әртүрлі деп саналатын жағдай – егер \((A_i, B_j)\) жұбы үшін \(A_i\) мен \(B_j\) арасындағы кесулердің саны айырмашылық көрсетсе. Назар аударыңыз: кесудің қалай жүргізілгені немесе олардың реті маңызды емес. Біз кесулерді біртіндеп иіп, созып не қысқартып, бір-бірімен қиылыспайтындай етіп өзгертуге болады деп есептейміз.

Енгізу

Бірінші және жалғыз жолда 2 сан бар: \(a\) және \(b\) (\(1 \le a, b \le 1000\)) – ішкі және сыртқы көпбұрыштардың өлшемдері. \(a + b \ge 3\) екендігіне кепілдік беріледі.

Шығару

Мәселенің жауабын шығарыңыз, себебі ол тым үлкен болуы мүмкін, сондықтан оны \(10^9 + 7\) модулімен шығарыңыз.

Мысалдар

Енгізу 1

1 2

Жауап 1

2

Енгізу 2

2 2

Жауап 2

6

Ескертпелер

Жарасхан сіздерге \(a = 2, b = 1\) жағдайында екі дұрыс кесудің мысалын сызды:

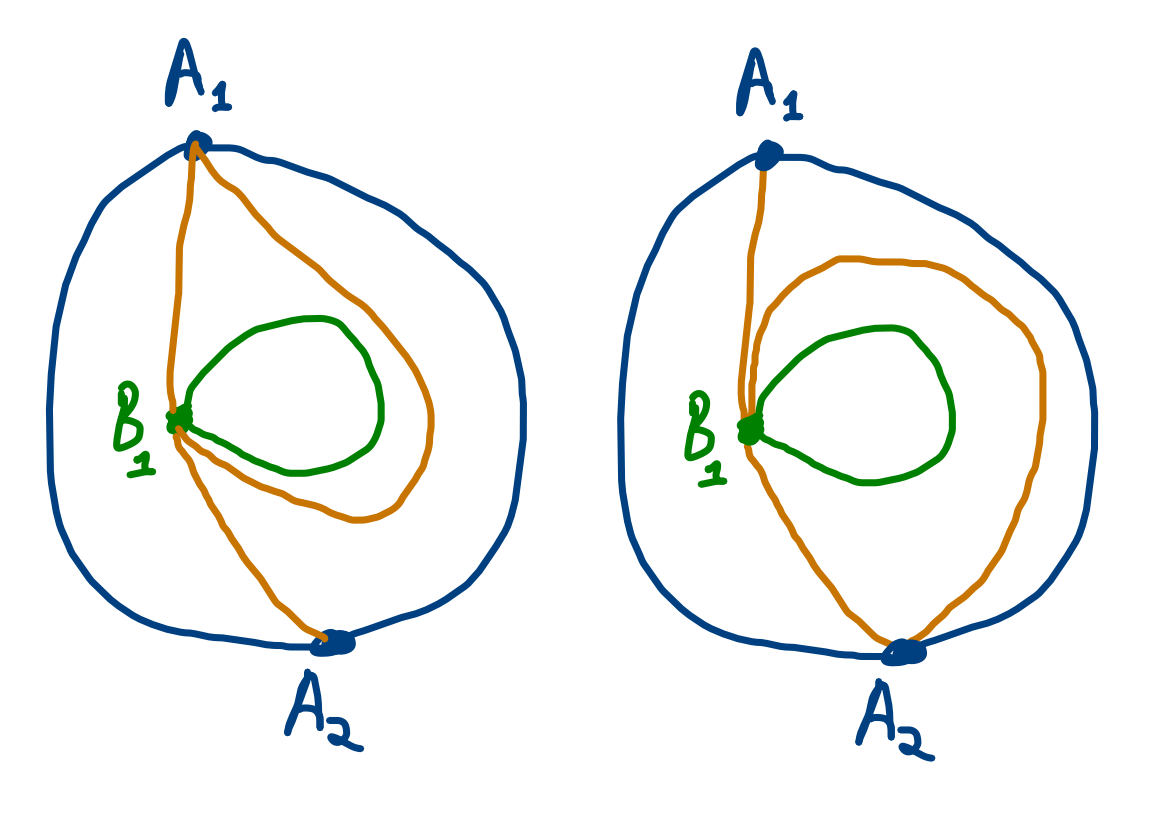
Әрбір соңғы бөлік 3 сызықпен шектеледі. Бірінші жағдайда, сағат тіліне қарсы тәртіпте:

• \(A_1 A_2 B_1\) – \(A_1 A_2\) жақтары, \(A_2 B_1\) кесуі және \(B_1 A_1\) кесуі;

• \(A_2 B_1 A_1\) – \(A_2 B_1\) кесуі, \(B_1 A_1\) кесуі және \(A_1 A_2\) жақтары;

• \(A_1 B_1 B_1\) – \(A_1 B_1\) кесуі, \(B_1 B_1\) (ішкі) жақтары және \(B_1 A_1\) кесуі.

Нәтижесінде 2 кесу \(A_1 B_1\) және 1 кесу \(B_1 A_2\).

Екінші жағдайда 2 кесу \(A_1 B_2\) және 1 кесу \(B_1 A_1\).

Бұл жағдайда басқа дұрыс кесулер жоқ.