Толық екілік дарақ — бұл дарақ түріндегі мәліметтер құрылымы. Ең төменгі деңгейде орналасқан және ұлдары жоқ жапырақтарды (дарақтың соңғы элементтері) қоспағанда, әрбір \(v\) шыңының әрқайсысында \(2v\) сол ұлы және \(2v+1\) оң ұлы бар. \(15\) шыңнан тұратын толық екілік дарақ:

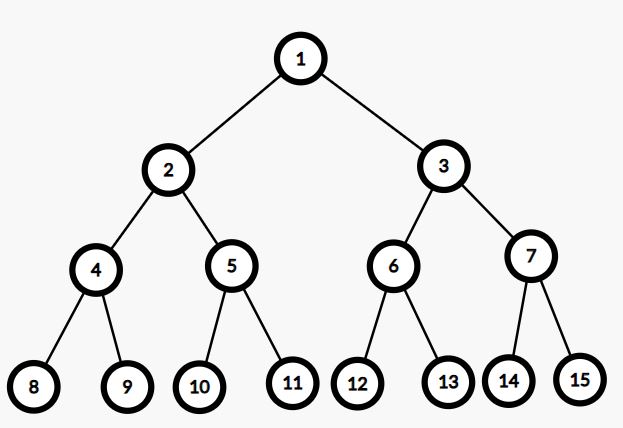
Тиманың \(n\) жапырағы бар толық екілік дарағы бар. Дарақтың әр жапырағында бүтін сан жазылған. Сондай-ақ оның шексіз көп \(min\), \(max\), \(sum\) жапсырмалары бар. Тима дарақтың ішкі (жапырақ емес) шыңдарының әрқайсысына бір жапсырма қоюды шешті.

Ол барлық жапсырмаларды орналастырғаннан кейін, ол дарақтың әр \(v\) шыңына \(f\) функциясы келесідей есептейді:

1. Егер \(v\) — жапырақ болса, онда \(f(v)\) \(v\) шыңында жазылған санға тең.

2. Егер \(v\) шыңында \(min\) жапсырмасы болса, онда \(f(v) = min(f(2*v), f(2*v+1))\).

3. Егер \(v\) шыңында \(max\) жапсырмасы болса, онда \(f(v) = max(f(2*v), f(2*v+1))\).

4. Егер \(v\) шыңында \(sum\) жапсырмасы болса, онда \(f(v) = f(2*v) + f(2*v+1)\).

Тима жапсырмаларды \(f(1)\) оның ең сүйікті \(x\) санына тең болатындай етіп орналастырғысы келеді. Оған көмектесіңіз.

Енгізу

Бірінші жолда \(n\) және \(x\) екі бүтін саны (\(2 \leq n \leq 131072\), \(1 \leq x \leq 131072\)) — жапырақтардың саны және Тиманың ең сүйікті саны берілген. \(n\) екінің дәрежесі екеніне кепілдік беріледі.

Екінші жолда \(n\) бүтін сандар \(a_1, a_2, \cdots, a_n\) (\(1 \leq a_i \leq 131072\)) — солдан оңға қарай жапырақтарда жазылған сандар, яғни сәйкесінше \(n, n+1, \cdots, 2n - 1\) шыңдарындағы сандар берілген.

Шығару

Егер жапсырмаларды \(f(1) = x\) етіп орналастыру мүмкін болмаса, онда «No» шығарыңыз.

Әйтпесе, бірінші жолда «Yes» және екінші жолда сәйкесінше \(1, 2, \cdots, n - 1\) шыңдарындағы жапсырмалардың мәндерін шығарыңыз.

Мысалдар

Енгізу 1

4 9
5 1 2 1

Жауап 1

Yes
sum sum sum

Енгізу 2

4 9
9 10 5 12

Жауап 2

Yes
min min max

Енгізу 3

8 10
5 6 12 8 3 1 5 11

Жауап 3

Yes
sum min min max min sum max