Ағаштағы ығыстырулар
Ағаш — бұл циклдері жоқ, байланысқан, бағытталмаған граф.
Сізге \(n\) төбеден тұратын ағаш берілген, және әрбір төбенің \(v\) салмағы \(w_v\) бар.
Төбенің кереметтігі оның көршілерінің салмақтарының қосындысына тең: \(c_v = \sum_{u \in g[v]} w_u\), — мұндағы \(g[v]\) — төбе \(v\)-нің көршілерінің тізімі.
Ағаштың кереметтігі — ерекше төбелердің кереметтіктерінің қосындысы. Ерекше төбелер — нөмірі \(L\)-ден \(R\)-ге дейінгі төбелер. Демек, ағаштың кереметтігі келесідей анықталады: \[C = \sum_{v=L}^{R} c_v.\]
Сізге келесі операцияны кез келген рет (соның ішінде 0 рет) орындауға рұқсат етіледі:
Кез келген төбе \(v\)-ны таңдау.
Төбе \(v\)-нің барлық көршілерінің \(w_u\) мәндерін \(g[v]\) тізімінде берілген ретпен циклдік ығыстыру. Яғни, егер \(g[v] = [u_1, u_2, \dots, u_k]\) болса, онда операциядан кейін:
Жаңа \(w_{u_1}\) ескі \(w_{u_2}\)-ге тең болады,
\(w_{u_2}\) ескі \(w_{u_3}\)-ке тең болады,
\(\dots\),
\(w_{u_k}\) ескі \(w_{u_1}\)-ге тең болады.
Есептің мақсат — осы операцияларды қолданып, ағаштың кереметтігі \(C\) мәнін мүмкіндігінше ең үлкен ету.
Енгізу
Бірінші жолда бүтін сан \(T\) (\(1 \le T \le 100\)) — тестілер саны.
Әрбір тест келесі түрде берілген:
Бірінші жолда бүтін сан \(n\) (\(1 \le n \le 5 \cdot 10^3\)) — ағаштағы төбелер саны.
Келесі жолда \(n\) бүтін сандары \(w_1, w_2, \dots, w_n\) (\(0 \le w_v \le 10^9\)) — төбелердің салмақтары.
Одан кейін \(n\) жол, мұнда \(v\)-ші жол алдымен бүтін сан \(k_v\) (\(0 \le k_v < n\)) — төбе \(v\)-нің көршілерінің саны, содан кейін \(k_v\) бүтін сандар — көршілерінің тізімі.
Соңғы жолда екі бүтін сан \(L\) және \(R\) (\(1 \le L \le R \le n\)) — ерекше төбелердің нөмірлерін анықтайтын аралық.
Кепілденеді, барлық тестілер үшін \(n\) сандарының қосындысы \(5 \cdot 10^3\)-тен аспайды және әрбір тест ағаш болып табылады.
Шығару
\(T\) жолды шығарыңыз, әр жолда бір бүтін сан — сипатталған операцияларды орындау арқылы қол жеткізуге болатын ағаштың кереметтігі \(C\)-нің ең үлкен мәні.
Бағалау жүйесі
Бұл есепте \(6\) ішкі есеп бар.
| Ішкі есеп | Қосымша шектеулер | Ұпайлар |
|---|---|---|
| \(0\) | Мысалдар | \(0\) |
| \(1\) | \(n \le 8\) | \(12\) |
| \(2\) | Тек бір ғана төбенің көршілерінің саны \(1\)-ден үлкен болуы мүмкін. | \(6\) |
| \(3\) | Барлық төбелерде көршілерінің саны \(2\)-ден аспайды. | \(9\) |
| \(4\) | \(L = R\) | \(15\) |
| \(5\) | \(n \le 50, T \le 10\) | \(24\) |
| \(6\) | — | \(34\) |
Мысалдар
Енгізу 1
2
6
9 3 7 9 7 0
3 4 5 3
1 6
1 1
1 1
2 1 6
2 5 2
4 6
5
2 3 2 3 9
2 3 4
1 4
2 1 5
2 1 2
1 3
1 3Жауап 1
34
20Ескертпелер
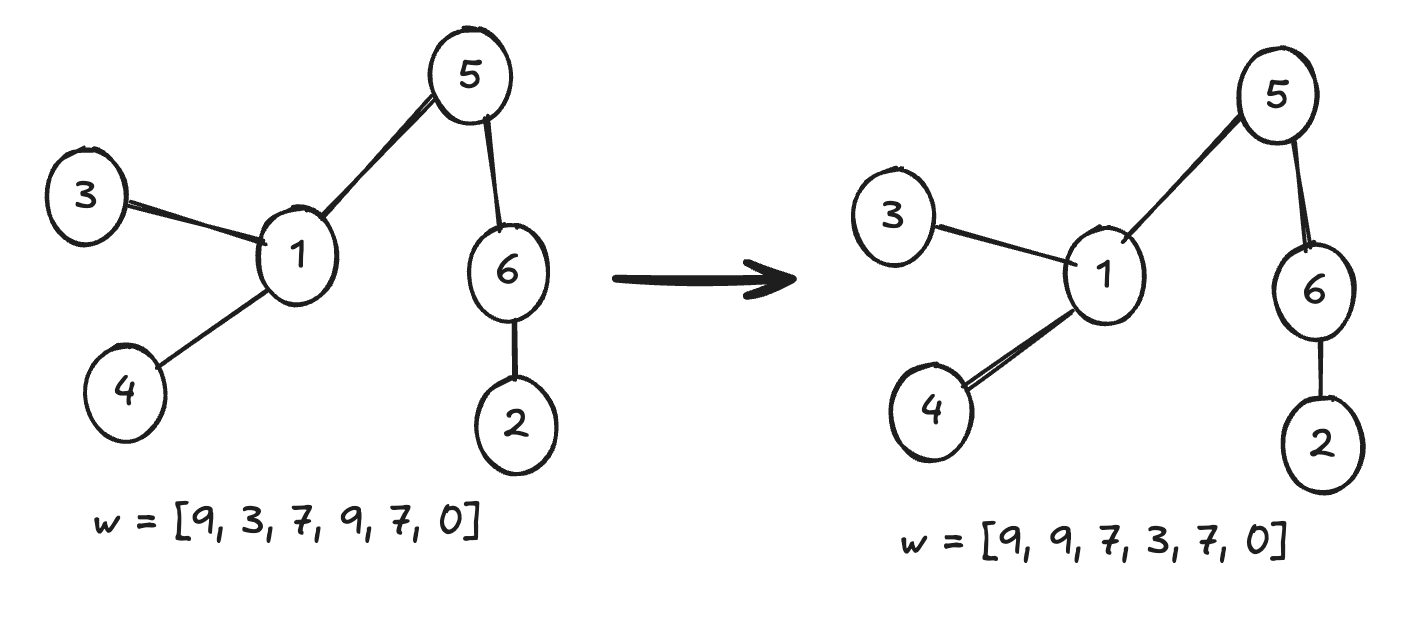
Бірінші мысалда жауап [\(1, 1, 6, 1\)] тәртібімен орындалатын операциялардан кейін қол жеткізіледі.
Пікірлер